Question:
Let $f(\mathrm{x})=15-|\mathrm{x}-10| ; \mathrm{x} \in \mathrm{R}$. Then the set of all values of $\mathrm{x}$, at which the function, $\mathrm{g}(\mathrm{x})=f(f(\mathrm{x}))$ is not differentiable, is :
Correct Option: , 3
Solution:
$f(\mathrm{x})=15-|\mathrm{x}-10|, \mathrm{x} \in \mathrm{R}$
$f(f(\mathrm{x}))=15-|f(\mathrm{x})-10|$
$=15-|15-| \mathrm{x}-10|-10|$
$=15-|5-| \mathrm{x}-10||$
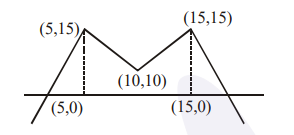
$x=5,10,15$ are points of non differentiability
Aliter :
At $\mathrm{x}=10 f(\mathrm{x})$ is non differentiable
also, when $15-|x-10|=10$
$\Rightarrow x=5,15$
$\therefore$ non differentiability points are $\{5,10,15\}$
