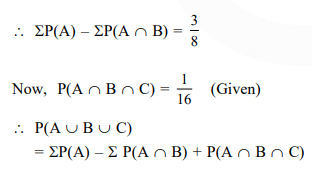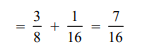Solve this following

For three events $A, B$ and $C$,

$P$ (Exactly one of $\mathrm{A}$ or $\mathrm{B}$ occurs)

$=\mathrm{P}($ Exactly one of $\mathrm{B}$ or $\mathrm{C}$ occurs $)$

$=\mathrm{P}($ Exactly one of $\mathrm{C}$ or A occurs $)=\frac{1}{4}$ and $\mathrm{P}($ All the three events occur simultaneously $)=\frac{1}{16}$.

Then the probability that at least one of the events occurs, is :-