Question:
Let $P$ and $Q$ be two distinct points on a circle which has center at $\mathrm{C}(2,3)$ and which passes through origin $\mathrm{O}$. If $\mathrm{OC}$ is perpendicular to both the line segments $\mathrm{CP}$ and $\mathrm{CQ}$, then the set $\{\mathrm{P}, \mathrm{Q}\}$ is equal to
Correct Option: , 4
Solution:
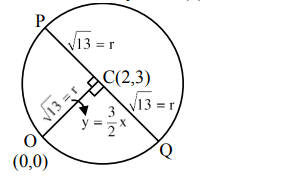
$\tan \theta=-\frac{2}{3}$
Using symmetric from of line
$P, Q:(2 \pm \sqrt{13} \cos \theta, 3 \pm \sqrt{13} \sin \theta)$
$\left(2 \pm \sqrt{13} \cdot\left(-\frac{3}{\sqrt{13}}\right), 3 \pm \sqrt{13}\left(\frac{2}{\sqrt{13}}\right)\right)$
$(-1,5) \&(5,1)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.