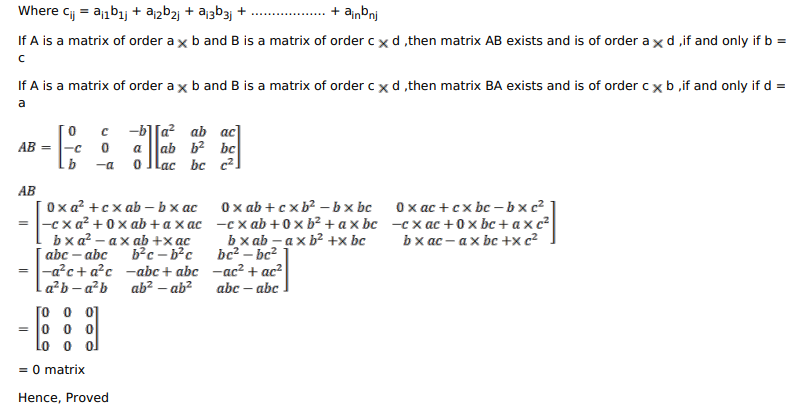Question:
If $A=\left[\begin{array}{ccc}0 & c & -b \\ -c & 0 & a \\ b & -a & 0\end{array}\right]$ and $B=\left[\begin{array}{ccc}a^{2} & a b & a c \\ a b & b^{2} & b c \\ a c & b c & c^{2}\end{array}\right]$, show that $A B$ is a zero matrix.
Solution:
Given : $\mathrm{A}=\left[\begin{array}{ccc}0 & \mathrm{c} & -\mathrm{b} \\ -\mathrm{c} & 0 & \mathrm{a} \\ \mathrm{b} & -\mathrm{a} & 0\end{array}\right]$ and $\mathrm{B}=\left[\begin{array}{ccc}\mathrm{a}^{2} & \mathrm{ab} & \mathrm{ac} \\ \mathrm{ab} & \mathrm{b}^{2} & \mathrm{bc} \\ \mathrm{ac} & \mathrm{bc} & \mathrm{c}^{2}\end{array}\right]$
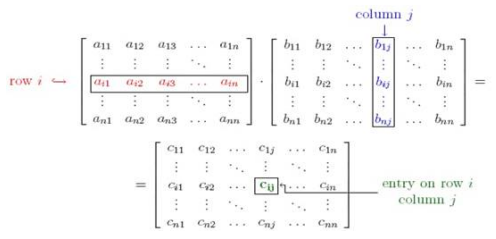
Matrix $A$ is of order $3 \times 3$, matrix $B$ is of order $3 \times 3$ and matrix $C$ is of order $3 \times 3$
To show : AB is a zero matrix