Three students $S_{1}, S_{2}$ and $S_{3}$ perform an experiment for determining the acceleration due to gravity (g) using a simple pendulum. They use different lengths of pendulum and record time for different number of oscillations. The observations are as shown in the table.
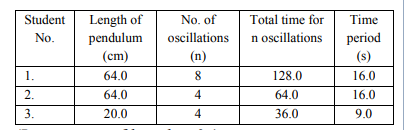
(Least count of length $=0.1 \mathrm{~m}$
least count for time $=0.1 \mathrm{~s}$ )
If $\mathrm{E}_{1}, \mathrm{E}_{2}$ and $\mathrm{E}_{3}$ are the percentage errors in ' $\mathrm{g}$ ' for students 1,2 and 3 respectively, then the minimum percentage error is obtained by student no.
$\mathrm{T}=2 \pi \sqrt{\frac{\ell}{\mathrm{g}}} \Rightarrow \mathrm{g}=\frac{4 \pi^{2} \ell}{\mathrm{T}^{2}}$
$\frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{\Delta \ell}{\ell}+\frac{2 \Delta \mathrm{T}}{\mathrm{T}}$
$\Delta \mathrm{T}=\frac{\text { least count of time }\left(\Delta \mathrm{T}_{0}\right)}{\text { number of oscillations }(\mathrm{n})}$
$\frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{\Delta \ell}{\ell}+\frac{2 \Delta \mathrm{T}_{0}}{\mathrm{nT}}$
As $\Delta \ell$ and $\Delta \mathrm{T}_{0}$ are same for all observations so
$\frac{\Delta \mathrm{g}}{\mathrm{g}}$ is minimum for highest value of $\ell, \mathrm{n}$ and $\mathrm{T}$
$\Rightarrow$ Minimum percentage error in $\mathrm{g}$ is for student number-1
