Question:
Let $\mathrm{f}:[0,3] \rightarrow \mathbf{R}$ be defined by
$f(x)=\min \{x-[x], 1+[x]-x\}$
where $[x]$ is the greatest integer less than or equal to $x$. Let $P$ denote the set containing all $x \in[0,3]$ where $\mathrm{f}$ is discontinuous, and $\mathrm{Q}$ denote the set containing all $x \in(0,3)$ where $f$ is not differentiable. Then the sum of number of elements in $P$ and $Q$ is equal to
Solution:
$1-\{x\}=1-x ; 0 \leq x<1$
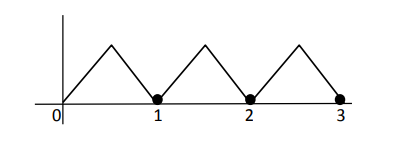
Non differentiable at
$x=\frac{1}{2}, 1, \frac{3}{2}, 2, \frac{5}{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.