Question:
A plane passing through the points $(0,-1,0)$
and $(0,0,1)$ and making an angle $\frac{\pi}{4}$ with the
plane $y-z+5=0$, also passes through the point
Correct Option: , 2
Solution:
Let $a x+b y+c z=1$ be the equation of the plane
$\Rightarrow 0-b+0=1$
$\Rightarrow b=-1$
$0+0+c=1$
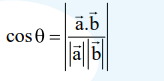
$\frac{1}{\sqrt{2}}=\frac{|0-1-1|}{\sqrt{\left(a^{2}+1+1\right)} \sqrt{0+1+1}}$
$\Rightarrow \mathrm{a}^{2}+2=4$
$\Rightarrow \mathrm{a}=\pm \sqrt{2}$
$\Rightarrow \pm \sqrt{2} \mathrm{x}-\mathrm{y}+\mathrm{z}=1$
Now for $-$ sign
$-\sqrt{2} \cdot \sqrt{2}-1+4=1$
option (2)
