Two sides of a parallelogram are along the lines $4 x+5 y=0$ and $7 x+2 y=0 .$ If the equation of one of the diagonals of the parallelogram is $11 x+7 y=9$, then other diagonal passes through the point:
Correct Option: , 2
Both the lines pass through origin.
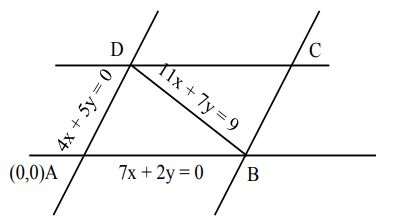
point $D$ is equal of intersection of $4 x+5 y=0 \&$ $11 x+7 y=9$
So, coordinates of point $\mathrm{D}=\left(\frac{5}{3},-\frac{4}{3}\right)$
Also, point B is point of intersection of $7 x+2 y=0$ $\& 11 x+7 y=9$
So, coordinates of point $\mathrm{B}=\left(-\frac{2}{3}, \frac{7}{3}\right)$
diagonals of parallelogram intersect at middle let middle point of $B, D$
$\Rightarrow\left(\frac{\frac{5}{3}-\frac{2}{3}}{2}, \frac{\frac{-4}{3}+\frac{7}{3}}{2}\right)=\left(\frac{1}{2}, \frac{1}{2}\right)$
equation of diagonal $\mathrm{AC}$
$\Rightarrow(\mathrm{y}-0)=\frac{\frac{1}{\alpha}-0}{\frac{1}{\alpha}-0}(\pi-0)$
$y=x$
diagonal AC passes through $(2,2)$
