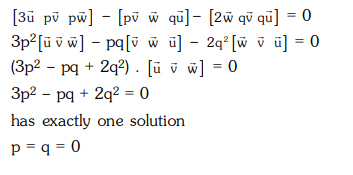Question:
If $\overrightarrow{\mathrm{u}}, \overrightarrow{\mathrm{v}}, \overrightarrow{\mathrm{w}}$ are non-coplanar vectors and $\mathrm{p}, \mathrm{q}$ are real numbers, then the equality
$[3 \overrightarrow{\mathrm{u}} \mathrm{p} \overrightarrow{\mathrm{v}} \mathrm{p} \overrightarrow{\mathrm{w}}]-[\mathrm{p} \overrightarrow{\mathrm{v}} \overrightarrow{\mathrm{w}} \mathrm{q} \overrightarrow{\mathrm{u}}]-[2 \overrightarrow{\mathrm{w}} \mathrm{q} \overrightarrow{\mathrm{v}} \mathrm{qu}]=0$ holds for :-
Correct Option: , 3
Solution:
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.