Question:
The area of the region bounded by $\mathrm{y}-\mathrm{x}=2$ and $\mathrm{x}^{2}=\mathrm{y}$ is equal to :-
Correct Option: , 3
Solution:
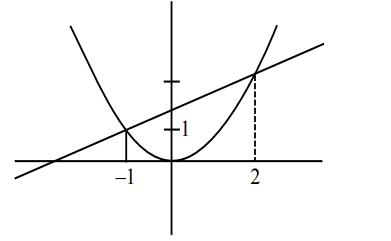
$y-x=2, x^{2}=y$
Now, $x^{2}=2+x$
$\Rightarrow x^{2}-x-2=0$
$\Rightarrow(x+1)(x-2)=0$
Area $=\int_{-1}^{2}\left(2+x-x^{2}\right)$
$=\left|2 x+\frac{x^{2}}{2}-\frac{x^{3}}{3}\right|_{-1}^{2}$
$=\left(4+2-\frac{8}{3}\right)-\left(-2+\frac{1}{2}+\frac{1}{3}\right)$
$=6-3+2-\frac{1}{2}=\frac{9}{2}$
