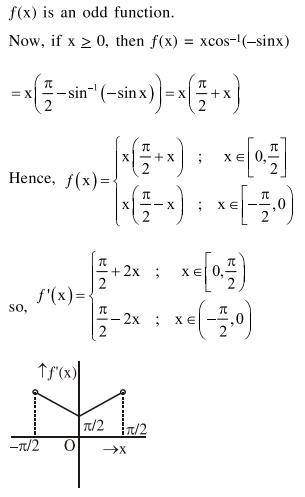Question: Let $f(x)=x \cos ^{-1}(-\sin |x|), x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$, then
which of the following is true ?
$f^{\prime}$ is decreasing in $\left(-\frac{\pi}{2}, 0\right)$ and increasing in $\left(0, \frac{\pi}{2}\right)$
$f$ is not differentiable at $x=0$
$f^{\prime}(0)=-\frac{\pi}{2}$
$f^{\prime}$ is increasing in $\left(-\frac{\pi}{2}, 0\right)$ and decreasing in $\left(0, \frac{\pi}{2}\right)$
Correct Option: 1
Solution: