Question:
Let $f:[0, \infty) \rightarrow[0,3]$ be a function defined by
$f(\mathrm{x})= \begin{cases}\max \{\sin \mathrm{t}: 0 \leq \mathrm{t} \leq \mathrm{x}\}, & 0 \leq \mathrm{x} \leq \pi \\ 2+\cos \mathrm{x}, & \mathrm{x}>\pi\end{cases}$
Then which of the following is true?
Correct Option: , 2
Solution:
Graph of $\max \{\sin t: 0 \leq t \leq x\}$ in $x \in[0, \pi]$
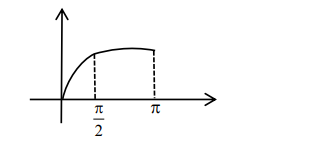
$\&$ graph of $\cos$ for $x \in[\pi, \infty)$
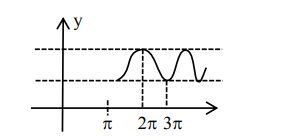
So graph of
$f(x)=\left\{\begin{array}{cc}\max \{\sin t: 0 \leq t \leq x, & 0 \leq x \leq \pi \\ 2+\cos x & x>h\end{array}\right.$
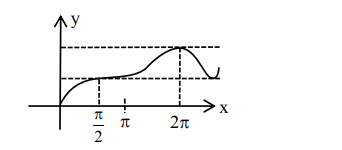
$\mathrm{f}(\mathrm{x})$ is differentiable everywhere in $(0, \infty)$
