Solve this

Let us consider a right $\triangle \mathrm{ABC}$ right angled at $\mathrm{B}$ and $\angle C=\theta$.

Now, we know that $\tan \theta=\frac{A B}{B C}=\frac{20}{21}$

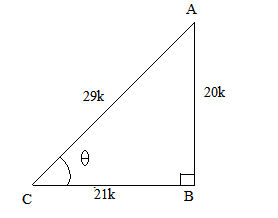
So, if AB = 20k, then BC = 21k, where k is a positive number.
Using Pythagoras theorem, we get:
 AC2 = AB2 + BC2
⇒ AC2= (20k)2 + (21k)2
⇒ AC2 = 841k2
⇒  AC = 29k

Now, $\sin \theta=\frac{A B}{A C}=\frac{20}{29}$ and $\cos \theta=\frac{B C}{A C}=\frac{21}{29}$

Substituting these values in the given expression, we get:

LHS $=\frac{1-\sin \theta+\cos \theta}{1+\sin \theta+\cos \theta}$

$=\frac{1-\frac{20}{29}+\frac{21}{29}}{1+\frac{20}{29}+\frac{21}{29}}$

$=\frac{\frac{29-20+21}{29}}{\frac{29+20+21}{29}}=\frac{30}{70}=\frac{3}{7}=$ RHS

∴ LHS = RHS

Hence proved.