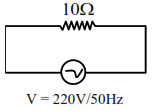
A $10 \Omega$ resistance is connected across $220 \mathrm{~V}-50 \mathrm{~Hz}$ AC supply. The time taken by the current to change from its maximum value to the rms value is:
Correct Option: 1
$\Rightarrow \mathrm{i}=\mathrm{i}_{0} \sin \omega \mathrm{t}$
When $\mathrm{i}=\mathrm{i}_{0}$
$\mathrm{i}_{0}=\mathrm{i}_{0} \sin \omega \mathrm{t}_{1} \Rightarrow \omega \mathrm{t}_{1}=\frac{\pi}{2} \ldots$ (i)
When $\mathrm{i}=\frac{\mathrm{i}_{0}}{\sqrt{2}}$
$\frac{\mathrm{i}_{0}}{\sqrt{2}}=\mathrm{i}_{0} \sin \omega \mathrm{t}_{2} \Rightarrow \omega \mathrm{t}_{2}=\frac{\pi}{4} \ldots$(ii)
Time taken by current from maximum value to $\mathrm{rms}$ value
$\Rightarrow\left(\mathrm{t}_{1}-\mathrm{t}_{2}\right)=\frac{\pi}{2 \omega}-\frac{\pi}{4 \omega}=\frac{\pi}{4 \omega}=\frac{\pi}{4 \times 2 \pi \mathrm{f}}$
$=\frac{1}{8 \times 50}$
$=\frac{1}{400} \mathrm{sec}$
$=2.5 \mathrm{~ms}$
