If $A(1,4), B(2,-3)$ and $C(-1,-2)$ are the vertices of a $\triangle A B C$, find the equation of
(i) the median through $\mathrm{A}$
(ii) the altitude through A
(iii) the perpendicular bisector of BC
Construction: Draw a line segment from vertex A intersecting BC at the midpoint (D).
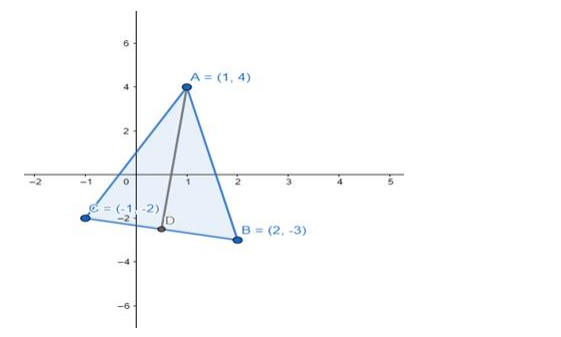
(i) Equation of median AD, we will find the midpoint of side BC
For side $\mathrm{BC}$ (midpoint $\mathrm{D}):(\mathrm{x}, \mathrm{y})=\frac{2+(-1)}{2}, \frac{-3+(-2)}{2}$
$(\mathrm{x}, \mathrm{y})=\left(\frac{1}{2}, \frac{-5}{2}\right)$
Now using two point form of the equation of the line, we have
Equation of side AD:
$y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\left(x-x_{1}\right)$
$y-4=\frac{\frac{-5}{2}-4}{\frac{1}{2}-1}(x-1) \Rightarrow y-4=\frac{\frac{-5-8}{2}}{\frac{1-2}{2}}(x-1)$
$y-4=\frac{-13}{-1}(x-1) \Rightarrow y-4=13 x-13$
$13 x-y-13+4=0$
$13 x-y-9=0$
So, required equation of altitude is $3 x-y-9=0$.
(ii) For the equation of altitude, we will need slope as we have a point through which line passes (A).
Now we will find the slope of side BC and using the relation between the slopes of perpendicular lines, i.e. $m_{1} \cdot m_{2}=-1$ we will find the slopes of altitude.
Slope of BC : $m_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \Rightarrow \frac{-2+(-3)}{-1-2}=\frac{-5}{-3}$
$\mathrm{m}_{1}=\frac{5}{3}$
Slope of $\mathrm{AM}: \mathrm{m}_{1} \cdot \mathrm{m}_{1}^{\prime}=-1 \Rightarrow \frac{5}{3} \cdot \mathrm{m}_{1}^{\prime}=-1$
$\mathrm{m}_{1}^{\prime}=\frac{-3}{5}$
Using slope intercept form, we will first calculate intercept,
y = mx + c ……………………(1)
$4=\frac{-3}{5}(1)+c \Rightarrow c=4+\frac{3}{5}$
$c=\frac{20+3}{5} \Rightarrow c=\frac{23}{5}$
Putting in equation (1)
$y=\frac{-3}{5} x+\frac{23}{5} \Rightarrow 3 x+5 y-23=0$
So, required equation of altitude is 3x + 5y - 23 = 0.
(iii) We have a slope of perpendicular and a mid point from the previous solution
$\mathrm{m}_{1}^{\prime}=\frac{-3}{5}$ midpoint of $\mathrm{BC}($ point $\mathrm{D})(\mathrm{x}, \mathrm{y})=\left(\frac{1}{2}, \frac{-5}{2}\right)$
Now for perpendicular bisector, it passes through the midpoint of BC, i.e. we have a slope of the equation and a point through which it passes so we can use the slope - intercept form and calculate intercept,
y = mx + c …………………(i)
$\frac{-5}{2}=\frac{-3}{5}\left(\frac{1}{2}\right)+c \Rightarrow c=\frac{-5}{2}+\frac{3}{10}$
$c=\frac{-25+3}{10} \Rightarrow c=\frac{-22}{10}$
$c=\frac{-11}{5}$
Putting in equation (i) value of c,
$y=\frac{-3}{5} x+\frac{-11}{5} \Rightarrow 3 x+y+11=0$
So, the required equation of perpendicular bisector is 3x + y + 11 = 0.
