Question:
The equation arg $\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}$ represents a circle with:
Correct Option: , 2
Solution:
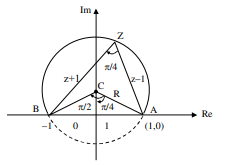
In $\triangle \mathrm{OAC}$
$\sin \left(\frac{\pi}{4}\right)=\frac{1}{\mathrm{AC}}$
$\Rightarrow \mathrm{AC}=\sqrt{2}$
Also, $\tan \frac{\pi}{4}=\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{1}{\mathrm{OC}}$
$\Rightarrow \mathrm{OC}=1$
$\therefore$ centre $(0,1) ;$ Radius $=\sqrt{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.