A cell $E_{1}$ of emf $6 \mathrm{~V}$ and internal resistance $2 \Omega$ is connected with another cell $\mathrm{E}_{2}$ of emf $4 \mathrm{~V}$ and internal resistance $8 \Omega$ (as shown in the figure).
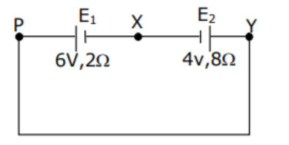
The potential difference across points $\mathrm{X}$ and $\mathrm{Y}$ is -
Correct Option: , 2
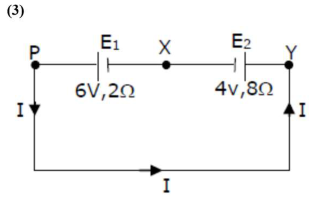
emf of $E_{1}=6 \mathrm{v}$
$r_{1}=2 \Omega$
$\operatorname{emf}$ of $E_{2}=4 \Omega$
$r_{2}=8 \Omega$
$\left|v_{x}-v_{y}\right|=$ potential difference across points $x$ and $y$
$E_{\text {eff }}=6-4=2 \mathrm{~V}$
$\mathrm{R}_{\text {eq }}=2+8=10 \Omega$
So, current in the circuit will be
$\Rightarrow \mathrm{I}=\frac{\mathrm{E}_{\mathrm{eff}}}{\mathrm{R}_{\mathrm{eq}}} \Rightarrow \mathrm{I}=\frac{2}{10}=0.2 \mathrm{~A}$
Now, potential difference across points $X$ and $Y$ is $\left|v_{x}-v_{y}\right|=E+i R$
$\Rightarrow\left|v_{x}-v_{y}\right|=4+0.2 \times 8=5.6 \mathrm{~V}$
$\Rightarrow\left|v_{x}-v_{y}\right|=5.6 v$
