In the figure of $\triangle \mathrm{PQR}, \angle \mathrm{P}=\theta^{\circ}$ and $\angle \mathrm{R}=\phi^{\circ}$. Find
(i) $(\sqrt{x+1}) \cot \phi$
(ii) $\left(\sqrt{x^{3}+x^{2}}\right) \tan \theta$
(iii) $\cos \theta$
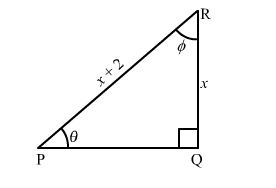
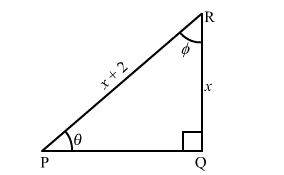
In $\triangle \mathrm{PQR}, \angle \mathrm{Q}=90^{\circ}$
Using Pythagoras theorem, we get
$\mathrm{PQ}=\sqrt{\mathrm{PR}^{2}-\mathrm{QR}^{2}}$
$=\sqrt{(x+2)^{2}-x^{2}}$
$=\sqrt{x^{2}+4 x+4-x^{2}}$
$=\sqrt{4(x+1)}$
$=2 \sqrt{x+1}$
Now,
(i) $(\sqrt{x+1}) \cot \phi$
$=(\sqrt{x+1}) \times \frac{\mathrm{QR}}{\mathrm{PQ}}$
$=(\sqrt{x+1}) \times \frac{x}{2 \sqrt{x+1}}$
$=\frac{x}{2}$
(ii) $\left(\sqrt{x^{3}+x^{2}}\right) \tan \theta$
$=\left(\sqrt{x^{2}(x+1)}\right) \times \frac{\mathrm{QR}}{\mathrm{PQ}}$
$=x \sqrt{(x+1)} \times \frac{x}{2 \sqrt{x+1}}$
$=\frac{x^{2}}{2}$
(iii) $\cos \theta$
$=\frac{\mathrm{PQ}}{\mathrm{PR}}$
$=\frac{2 \sqrt{x+1}}{(x+2)}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.