Solve this

We have, $A=\left[\begin{array}{lll}3 & -3 & 4\end{array}\right.$

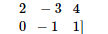
$A^{2}=\left[\begin{array}{lll}3 & -3 & 4\end{array}\right.$

$\begin{array}{lll}2 & -3 & 4\end{array}$

$0-1 \quad 1 \quad 1]\left[\begin{array}{lll}3 & -3 & 4\end{array}\right.$

$2 \quad-3 \quad 4$

$0-1 \quad 1]=\left[\begin{array}{lll}9-6+0 & -9+9-4 & 12-12+4\end{array}\right.$

$6-6+0 \quad-6+9-4 \quad 8-12+4$

$0-2+0 \quad 0+3-1 \quad 0-4+1]=\left[\begin{array}{lll}3 & -4 & 4\end{array}\right.$

$\begin{array}{lll}0 & -1 & 0\end{array}$

$\begin{array}{lll}-2 & 2 & -3]\end{array}$

Now, $A^{3}=A^{2} \times A=\left[\begin{array}{lll}3 & -4 & 4\end{array}\right.$

$\begin{array}{lll}0 & -1 & 0\end{array}$

$\left.\begin{array}{lll}-2 & 2 & -3\end{array}\right]\left[\begin{array}{lll}3 & -3 & 4\end{array}\right.$

$\begin{array}{lll}2 & -3 & 4\end{array}$

$0-1 \quad 1]=\left[\begin{array}{lll}9-8 & -9+12-4 & 12-16+4\end{array}\right.$

$\begin{array}{lll}0-2+0 & 0+3+0 & -4\end{array}$

$-6+4+0 \quad 6-6+3 \quad-8+8-3]=\left[\begin{array}{lll}1 & -1 & 0\end{array}\right.$

$\left.\begin{array}{lll}-2 & 3 & -3\end{array}\right]$

$-2 \quad 3 \quad-3]$

Again $A^{3} \times A=\left[\begin{array}{lll}1 & -1 & 0\end{array}\right.$

$\begin{array}{lll}-2 & 3 & -4\end{array}$

$\left.\begin{array}{lll}-2 & 3 & -3\end{array}\right]\left[\begin{array}{lll}3 & -3 & 4\end{array}\right.$

$\begin{array}{lll}2 & -3 & 4\end{array}$

$\left.\begin{array}{lll}0 & -1 & 1\end{array}\right]=\left[\begin{array}{llllllll}3-2+0 & -3+3+0 & 4-4+0-6+6 & 6-9+4 & -8+12-4 & 0 & 0 & 1\end{array}\right]$

$=\left[\begin{array}{lll}1 & 0 & 0\end{array}\right.$

$\begin{array}{lll}0 & 1 & 0\end{array}$

$\begin{array}{lll}0 & 0 & 1]=I_{3} \quad[\text { Identity matrix of order } 3]\end{array}$

$\Rightarrow A^{3} \times A=I_{3}$

$\Rightarrow A^{3}=A^{-1}$