Let $A=\left[\begin{array}{ccc}1 & \sin \theta & 1 \\ -\sin \theta & 1 & \sin \theta \\ -1 & -\sin \theta & 1\end{array}\right]$, where $0 \leq \theta \leq 2 \pi$. Then,
(a) Det $(A)=0$
(b) Det $(A) \in(2, \infty)$
(c) Det $(A) \in(2,4)$
(d) Det $(A) \in[2,4]$
(d) $\operatorname{Det}(A) \in[2,4]$
$\mid \begin{array}{lll}1 & \sin \theta & 1\end{array}$
$-\sin \theta \quad 1 \quad \sin \theta$
$\begin{array}{lll}-1 & -\sin \theta & 1 \mid\end{array}$
$=\mid \begin{array}{lll}1 & \sin \theta & 2\end{array}$
$\begin{array}{lll}-\sin \theta & 1 & 0\end{array}$
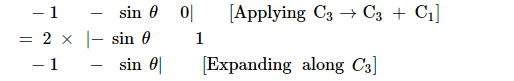
$=2\left(\sin ^{2} \theta+1\right)$
Given : $0 \leq \theta \leq 2 \pi$
$\Rightarrow-1 \leq \sin \theta \leq 1$
$\Rightarrow 0 \leq \sin ^{2} \theta \leq 1$
$|\mathrm{A}|=2\left(\sin ^{2} \theta+1\right)$
$|\mathrm{A}|=2 \times 1=2 \quad[\theta=0]$
$=2 \times 2=4 \quad[\theta=2 \pi]$
$\Rightarrow \operatorname{Det}(\mathrm{A}) \in[2,4]$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.