Solve this

$A=\left[\begin{array}{lll}1 & 2 & 2\end{array}\right.$

$\begin{array}{lll}2 & 1 & 2\end{array}$

$\left.\begin{array}{lll}2 & 2 & 1\end{array}\right]$

$\Rightarrow|A|=\mid \begin{array}{lll}1 & 2 & 2\end{array}$

$\begin{array}{lll}2 & 1 & 2\end{array}$

$2 \quad 2 \quad 1 \mid=1(1-4)-2(2-4)+2(4-2)=-3+4+4=5$

Since, $|A| \neq 0$

Hence, $A$ is invertible.

Now,

$A^{2}=\left[\begin{array}{lll}1 & 2 & 2\end{array}\right.$

$\begin{array}{lll}2 & 1 & 2\end{array}$

$\left.\begin{array}{lll}2 & 2 & 1\end{array}\right]\left[\begin{array}{lll}1 & 2 & 2\end{array}\right.$

$\begin{array}{lll}2 & 1 & 2\end{array}$

$\left.\begin{array}{lll}2 & 2 & 1\end{array}\right]=\left[\begin{array}{lll}1+4+4 & 2+2+4 & 2+4+2\end{array}\right.$

$2+2+4 \quad 4+1+4 \quad 4+2+2$

$2+4+2 \quad 4+2+2 \quad 1+4+4]=\left[\begin{array}{lll}9 & 8 & 8\end{array}\right.$

Now, $A^{2}-4 A-5 I=\left[\begin{array}{lll}9 & 8 & 8\end{array}\right.$

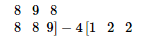
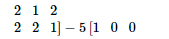
$\left.\begin{array}{lll}0 & 0 & 1\end{array}\right]=\left[\begin{array}{lll}9-4-5 & 8-8-0 & 8-8-0\end{array}\right.$

$\begin{array}{lll}8-8-0 & 9-4-5 & 8-8-0\end{array}$

$8-8-0 \quad 8-8-0 \quad 9-4-5]=\left[\begin{array}{lll}0 & 0 & 0\end{array}\right.$

$\begin{array}{lll}0 & 0 & 0\end{array}$

$\left.\begin{array}{lll}0 & 0 & 0\end{array}\right]=O$

$\Rightarrow A^{2}-4 A-5 I=O \quad[$ Proved $]$

Again, $A^{2}-4 A-5 I=O$

$\Rightarrow A^{-1}\left(A^{2}-4 A-5 I\right)=A^{-1} O \quad\left[\right.$ Pre $-$ multiplying with $\left.A^{-1}\right]$

$\Rightarrow A-4 I=5 A^{-1}$

$\Rightarrow 5 A^{-1}=\left[\begin{array}{lll}1 & 2 & 2\end{array}\right.$

$\begin{array}{lll}2 & 1 & 2\end{array}$

$2 \quad 2 \quad 1]-4\left[\begin{array}{lll}1 & 0 & 0\end{array}\right.$

$\begin{array}{lll}0 & 1 & 0\end{array}$

$\left.\begin{array}{lll}0 & 0 & 1\end{array}\right]=\left[\begin{array}{lll}1-4 & 2-0 & 2-0\end{array}\right.$

$2-0 \quad 1-4 \quad 2-0$

$\left.\begin{array}{lll}2-0 & 2-0 & 1-4\end{array}\right]=\left[\begin{array}{lll}-3 & 2 & 2\end{array}\right.$

$\begin{array}{lll}2 & -3 & 2\end{array}$

$\Rightarrow A^{-1}=\frac{1}{5}\left[\begin{array}{lll}-3 & 2 & 2\end{array}\right.$

$\left.\begin{array}{lll}2 & 2 & -3\end{array}\right]$

$\begin{array}{lll}2 & -3 & 2\end{array}$

$\Rightarrow A^{-1} A^{2}-4 A^{-1} A-5 A^{-1}=O$