Solve this

Let us first draw a right $\triangle \mathrm{ABC}$, right angled at $\mathrm{B}$ and $\angle C=\theta$.

Now, we know that $\cos \theta=\frac{\text { Base }}{\text { hypotenuse }}=\frac{B C}{A C}=\frac{7}{25}$.

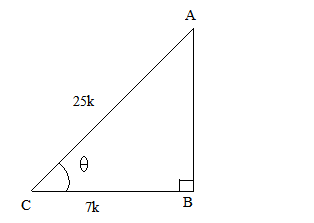
So, if BC = 7k, then AC = 25k, where k is a positive number.
Now, using Pythagoras theorem, we have:
AC2 = AB2 + BC2 
⇒ AB2 = AC2 -">−- BC2 = (25k)2 -">−- (7k)2.
⇒ AB2 = 625k2 -">−- 49k2 = 576k2
⇒ AB = 24k
Now, finding the other trigonometric ratios using their definitions, we get:

$\sin \theta=\frac{A B}{A C}=\frac{24 k}{25 k}=\frac{24}{25}$

$\tan \theta=\frac{A B}{B C}=\frac{24 k}{7 k}=\frac{24}{7}$

$\therefore \cot \theta=\frac{1}{\tan \theta}=\frac{7}{24}, \operatorname{cosec} \theta=\frac{1}{\sin \theta}=\frac{25}{24}$ and $\sec \theta=\frac{1}{\cos \theta}=\frac{25}{7}$