Wires $\mathrm{W}_{1}$ and $\mathrm{W}_{2}$ are made of same material having the breaking stress of $1.25 \times 10^{9} \mathrm{~N} / \mathrm{m}^{2}$.
$\mathrm{W}_{1}$ and $\mathrm{W}_{2}$ have cross-sectional area of $8 \times 10^{-7} \mathrm{~m}^{2}$ and $4 \times 10^{-7} \mathrm{~m}^{2}$, respectively. Masses of $20 \mathrm{~kg}$ and $10 \mathrm{~kg}$ hang from them as shown in the figure. The maximum mass that can be placed in the pan without breaking the wires is $\mathrm{kg} _________.$ (Use $g=10 \mathrm{~m} / \mathrm{s}^{2}$ )
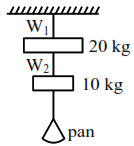
B.S $_{1}=\frac{\mathrm{T}_{1 \max }}{8 \times 10^{-7}} \Rightarrow \mathrm{T}_{1 \mathrm{max}}=8 \times 1.25 \times 100$
$=1000 \mathrm{~N}$
B.S ${ }_{2}=\frac{\mathrm{T}_{2 \max }}{4 \times 10^{-7}} \Rightarrow \mathrm{T}_{2 \max }=4 \times 1.25 \times 100$
$=500 \mathrm{~N}$
$\mathrm{m}=\frac{500-100}{10}=40 \mathrm{~kg}$
