Question:
If $A=\left[\begin{array}{lll}a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & a\end{array}\right]$, then the value of $|\operatorname{adj} A|$ is
(a) $a^{27}$
(b) $a^{9}$
(c) $a^{6}$
(d) $a^{2}$
Solution:
(c) $a^{6}$
$A=\left[\begin{array}{lll}a & 0 & 0\end{array}\right.$
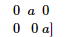
$\therefore|A|=\mid a \quad 0 \quad 0$
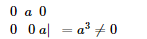
and
$n=3$
Thus, we have
$|\operatorname{adj} A|=|A|^{n-1}=\left(a^{3}\right)^{2}=a^{6}$
