Three containers $C_{1}, C_{2}$ and $C_{3}$ have water at different temperatures. The table below shows the final temperature $T$ when different amounts of water (given in liters) are taken from each container and mixed (assume no loss of heat during the process)
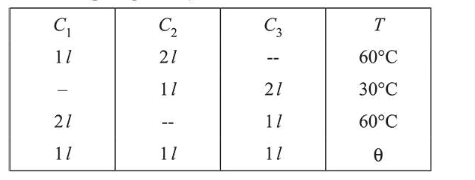
The value of $\theta$ (in ${ }^{\circ} \mathrm{C}$ to the nearest integer) is
$(\mathbf{5 0 . 0 0})$
Let $Q_{1}, Q_{2}, Q_{3}$ be the temperatures of container $C_{1}, C_{2}$ and $\mathrm{C}_{3}$ respectively.
Using principle of calorimetry in container $C_{1}$, we have
$\left(\theta_{1}-60\right)=2 \mathrm{~ms}(60-\theta)$
$\Rightarrow \theta_{1}-60=120-2 \theta$
$\Rightarrow \theta_{1}=180-2 \theta$ ....(i)
For container $C_{2}$
$\mathrm{ms}\left(\theta_{2}-30\right)=2 \mathrm{~ms}(30-\theta)$
$\Rightarrow \theta_{2}=90-2 \theta 3$ ...(2)
For container $\mathrm{C}_{3}$
$2 \mathrm{~ms}\left(\theta_{1}-60\right)=\mathrm{ms}(60-\theta)$
$\Rightarrow 2 \theta_{1}-120=60-\theta$
$\Rightarrow 2 \theta_{1}+\theta=180$ ....(3)
Also, $\theta_{1}+\theta_{2}+\theta_{3}=3 \theta$ .....(4)
Adding (i), (ii) and (iii)
$3 \theta_{1}+3 \theta_{2}+3 \theta_{3}=450$
$\Rightarrow \theta_{1}+\theta_{2}+\theta_{3}=150$
$\Rightarrow 3 \theta=150 \Rightarrow \theta=50^{\circ} \mathrm{C}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.