Solve the following systems of equations:

The given equations are:

$\frac{1}{5 x}+\frac{1}{6 y}=12$$\ldots(i)$

$\frac{1}{3 x}-\frac{3}{7 y}=8$...(ii)

Multiply equation $(i)$ by $\frac{3}{7}$ and equation (ii) by $\frac{1}{6}$, add both equations, we get

$\frac{3}{35 x}+\frac{3}{42 y}=\frac{36}{7}$

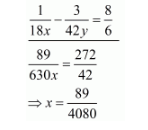
Put the value of $x$ in equation $(i)$, we get

$\frac{1}{\frac{5 \times 89}{4080}}+\frac{1}{6 y}=12$

$\Rightarrow \frac{1}{6 y}=\frac{1260}{445}$

$\Rightarrow y=\frac{89}{1512}$

Hence the value of $x=\frac{89}{4080}$ and $y=\frac{89}{1512}$