Solve the following systems of equations:

The given equations are:

$\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}$

$\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=-\frac{1}{8}$

Let $\frac{1}{3 x+y}=u$ and $\frac{1}{3 x-y}=v$ then equations are

$u+v=\frac{3}{4} \ldots(i)$

$\frac{u}{2}-\frac{v}{2}=\frac{1}{8} \ldots$- (ii)

Multiply equation (ii) by 2 and add both equations, we get

$u+v=\frac{3}{4}$

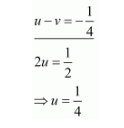
Put the value of $u$ in equation $(i)$, we get

$1 \times \frac{1}{4}+v=\frac{3}{4}$

$\Rightarrow v=\frac{1}{2}$

Then 

$\frac{1}{3 x+y}=\frac{1}{4}$$\ldots($ iii $)$

$\Rightarrow 3 x+y=4$

$\frac{1}{3 x-y}=\frac{1}{2}$$\therefore(i v)$

$\Rightarrow 3 x-y=2$

Add both equations, we get

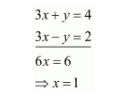
Put the value of $x$ in equation (iii) we get

$3 \times 1+y=4$

$\Rightarrow y=1$

Hence the value of $x=1$ and $y=1$