Question:
Solve the following system of inequalities graphically: x + y≥ 4, 2x – y > 0
Solution:
$x+y \geq 4 \ldots(1)$
$2 x-y>0 \ldots(2)$
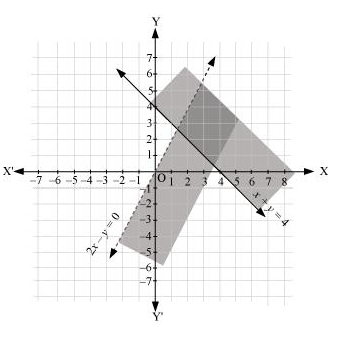
The graph of the lines, $x+y=4$ and $2 x-y=0$, are drawn in the figure below.
Inequality (1) represents the region above the line, $x+y=4$ (including the line $x+y=4$ ).
It is observed that $(1,0)$ satisfies the inequality, $2 x-y>0$. [2(1) $-0=2>0$ ]
Therefore, inequality (2) represents the half plane corresponding to the line, $2 x-y=0$, containing the point $(1,0)$ [excluding the line $2 x-y>0$ ].
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on line x + y = 4 and excluding the points on line 2x – y = 0 as follows.