If $\alpha$ and $\beta$ are the distinct roots of the equation $x^{2}+(3)^{1 / 4} x+3^{1 / 2}=0$, then the value of $\alpha^{96}\left(\alpha^{12}-1\right)+\beta^{96}\left(\beta^{12}-1\right)$ is equal to :
Correct Option: , 3
As, $\left(\alpha^{2}+\sqrt{3}\right)=-(3)^{1 / 4} \cdot \alpha$
$\Rightarrow\left(\alpha^{4}+2 \sqrt{3} \alpha^{2}+3\right)=\sqrt{3} \alpha^{2}$ (On squaring)
$\therefore\left(\alpha^{4}+3\right)=(-) \sqrt{3} \alpha^{2}$
$\Rightarrow \alpha^{8}+6 \alpha^{4}+9=3 \alpha^{4} \quad$ (Again squaring)
$\therefore \alpha^{8}+3 \alpha^{4}+9=0$
$\Rightarrow \alpha^{8}=-9-3 \alpha^{4}$
(Multiply by $\alpha^{4}$ )
So, $\alpha^{12}=-9 \alpha^{4}-3 \alpha^{8}$
$\therefore \quad \alpha^{12}=-9 \alpha^{4}-3\left(-9-3 \alpha^{4}\right)$
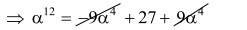
Hence, $\alpha^{12}=(27)^{2}$
