Question:
Let $\mathrm{P}_{1}, \mathrm{P}_{2}, \ldots, \mathrm{P}_{15}$ be 15 points on a circle. The number of distinct triangles formed by points $P_{i}, P_{j}, P_{k}$ such that $i+j+k \neq 15$, is :
Correct Option: , 3
Solution:
Total Number of Triangles $={ }^{15} \mathrm{C}_{3}$
$\mathrm{i}+\mathrm{j}+\mathrm{k}=15$ (Given)
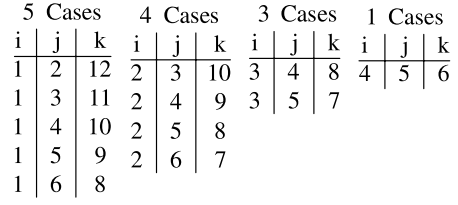
Number of Possible triangles using the vertices $\mathrm{P}_{\mathrm{i}}, \mathrm{P}_{\mathrm{j}}$, $P_{k}$ such that $i+j+k \neq 15$ is equal to ${ }^{15} C_{3}-12=443$
Option (3)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.