Solve the following equations

$A_{r}=\mid 1 \quad r \quad 2^{r}$

$\begin{array}{lll}2 & n & n^{2}\end{array}$

$n \quad \frac{n(n+1)}{2} \quad 2^{n+1} \mid$

$\Rightarrow \sum_{r=1}^{n} A_{r}=\mid \sum_{r=1}^{n} 1 \quad \sum_{r=1}^{n} r \quad \sum_{r=1}^{n} 2^{r} \sum_{r=1}^{n} 2 \quad n \quad n \quad n^{2} n \quad \frac{n(n+1)}{2}$

As $\sum_{r=1}^{n} 1=1+1+1 \ldots+1(n$ times $)=n$

$\sum_{r=1}^{n} r=1+2+3+\ldots+n=\frac{n(n+1)}{2}$

Let $S=\sum_{r=1}^{n} 2^{r}=2+2^{2}+2^{3}=\ldots+2^{n}$

$2 S=2^{2}+2^{3}=\ldots+2^{n}+2^{n+1}$

$\Rightarrow 2 S-S=S=\sum_{r=1}^{n} 2^{r}=2^{n+1}-2$

$\Rightarrow \sum_{r=1}^{n} A_{r}=\mid n \quad \frac{n(n+1)}{2} \quad 2^{n+1}-2$

$2 n \quad n \quad n^{2}$

$n \quad \frac{n(n+1)}{2}$ $2^{n+1} \mid$

[Applying $R_{1} \rightarrow R_{1}-R_{2}$ ]

$\sum_{r=1}^{n} A_{r}$

$=\left|n-n \quad \frac{n(n+1)}{2}-\frac{n(n+1)}{2} \quad 2^{n+1}-2-2^{n+1} 2 n \quad n \quad n^{2} n \quad \frac{n(n+1)}{2} \quad 2^{n+1}\right|$

$=\mid \begin{array}{lll}0 & 0 & -2\end{array}$

$\begin{array}{lll}2 n & n & n^{2}\end{array}$

$n \quad \frac{n(n+1)}{2}$ $2^{n+1} \mid$

$=-2 \times \mid 2 n$   $n$

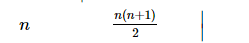
$=-2\left[n^{3}+n^{2}-n^{2}\right]$

$=-2 n^{3}$