Question:
Three particles, each of mass $200 \mathrm{~g}$, are kept at the corners of an equilateral triangle of side $10 \mathrm{~cm}$. Find the moment of inertia of the system about an axis
(a) joining two of the particles and
(b) passing through one of the particles and perpendicular to the plane of the particles.
Solution:
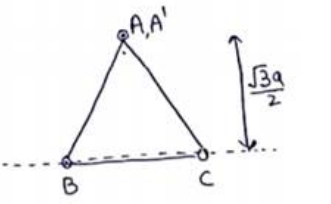
(a) $I_{B C}=m^{\left(\frac{\sqrt{3}}{2} a\right)^{2}+m(0)^{2}+m(0)^{2}}$
$=0.2^{\left(\frac{\sqrt{3}}{2} \times 0.1\right)^{2}}$
$=1.5^{\times 10^{-3}} \mathrm{Kq}_{-} m^{2}$
(b) $I_{A A^{r}}=m(0)^{2}+m(a)^{2}+m(0)^{2}$
$=2 \times 0.2(0.1)^{2}$
$=4^{\times 10^{-3}} \mathrm{Kg}_{-} \mathrm{m}^{2}$
