Solve the following :

Question:

Suppose the rod in the previous problem has a mass of $1 \mathrm{~kg}$ distributed uniformly over its length.

(a) Find the initial angular acceleration of the rod.

(b) Find the tension in the supports to the blocks of mass $2 \mathrm{~kg}$ and $5 \mathrm{~kg}$.

Solution:

(a) $\tau=I \alpha$

$(50 \times 0.5-20 \times 0.5)=\left[(2)^{(0.5)^{2}}+5^{(0.5)^{2}}+\frac{(1)(1)^{2}}{12}\right] \alpha$

$\alpha=8.1 \frac{\operatorname{rad}}{\sec ^{2}}$

(b)

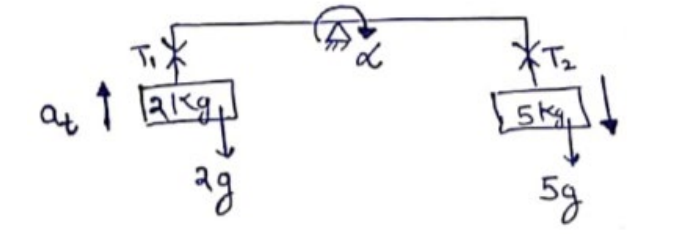
$a_{t}=R \alpha=(0.5)(8) \approx 4$

$T_{1}-2 g=2 . a_{t}$

$T_{1}=2(9.8)+2(4)$

$T_{1}=27.6 \mathrm{~N}$

$5 g-T_{2}=5 a_{t}$

$T_{2}=5(9.8)-5(4)$

$T_{2}=29 \mathrm{~N}$

Leave a comment

None

All Study Material

Free Study Material