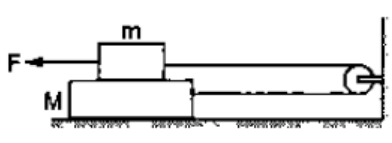
Consider the situation shown in figure. Suppose a small electric field Eexists in the space in the vertically upward direction and the upper block carries a positive charge $Q$ on its top surface. The friction coefficient between the two blocks is $g$ but the floor is smooth. What maximum horizontal force Fcan be applied without disturbing the equilibrium?
[Hint: The force on a charge $Q$ by the electric field $E$ is $F=Q E$ in the direction of $E$.]
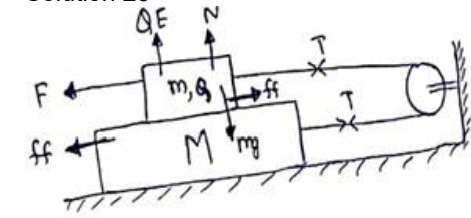
For block $\mathrm{m}$,
$\mathrm{QE}+\mathrm{N}=\mathrm{mg}$ (vertical equilibrium)
$\mathrm{N}=\mathrm{mg}-\mathrm{QE}$
$f f=\mu N=\mu(m g-Q E)$
$\mathrm{F}=\mathrm{T}+\mathrm{ff}$ (Horizontal equilibrium) -(i)
For block M,
T=ff (Horizontal Equilibrium) -(ii)
Solving (i)and(ii),
$F=f f+f t$
$F=2 f f=2 \mu(m g-Q E)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.