A uniform ladder of length $10.0 \mathrm{~m}$ and mass $16.0 \mathrm{~kg}$ is resting against a vertical wall making an angle of $37^{\circ}$ with it. The vertical wall is frictionless but the ground is rough. An electrician weighing $60.0 \mathrm{~kg}$ climbs up the ladder. If he stays on the ladder at a point $8.00 \mathrm{~m}$ from the lower end, what will be the normal force and the force of friction on the ladder by the ground? What should be the minimum coefficient of friction for the electrician to work safely?
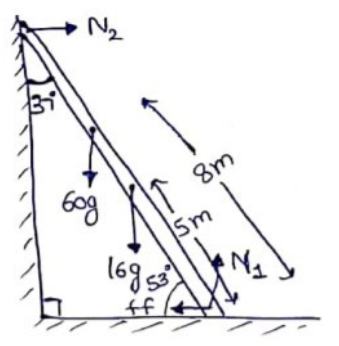
Translatory Equilibrium Equation
$N_{2}=f f$
$N_{1}=60 g+16 g$
$N_{1}=76 g=745 \mathrm{~N}$
Rotational Equilibrium at bottom of ladder Clockwise Torque =Anticlockwise Torque
$N_{2}\left(10 \cos 37^{\circ}\right)=16 g(5 \sin 53)+60 g(8 \sin 53)$
Solving, $N_{2}=412 \mathrm{~N}$
$f f=N_{2}=412=\mu N_{1}$
412= $\mu(76 g)$
$412=\mu(76 g)$ $\mu=0.553$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.