Question:
Find the moment of inertia of a uniform square plate of mass $m$ and edge a about one of its diagonals.
Solution:
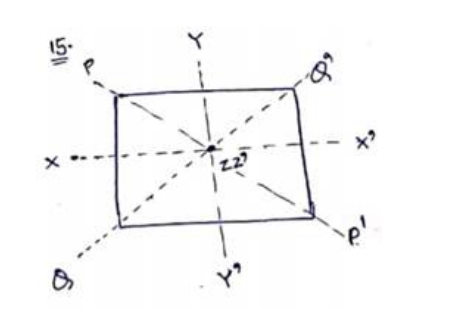
If we squeeze rod along $X X^{v}$ and $Y Y^{v}$ the square becomes rod of side 'a' So,
$I_{X X^{r}}=I_{Y Y^{r}}=\frac{m a^{2}}{12}$
By perpendicular axis theorem,
$I_{Z Z^{r}}=I_{X X^{l}}+I_{Y Y^{r}}=I_{p p^{l}}+I_{Q Q^{l}}$
$\frac{m a^{2}}{12}+\frac{m a^{2}}{12}=I_{p p^{l}}+I_{Q Q^{\prime}}$
$I_{p p^{l}}=\frac{m a^{2}}{12}\left[\because_{p p^{l}}=I_{Q Q^{\prime}}\right.$ As square is symmetric $]$
