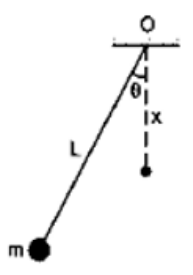
A simple pendulum of length $L$ having a bob of mass $m$ is deflected from its rest position by an angle 9 and released (figure 8-E16). The string hits a peg which is fixed at a distance $x$ below the point of suspension and the bob starts going in a circle centred at the peg. (a) Assuming that initially the bob has a height less than the peg, show that the maximum height reached by the bob equals its initial height. (b) If the pendulum is released with $\theta=90^{\circ}$ and $x=L / 2$ find the maximum height reached by the bob above its lowest position before the string becomes slack. (c) Find the minimum value of $x / L$ for which the bob goes in a complete circle about the peg when the pendulum is released from $\theta=$ $90^{\circ}$.
Total energy at $A$ and $B$ are same
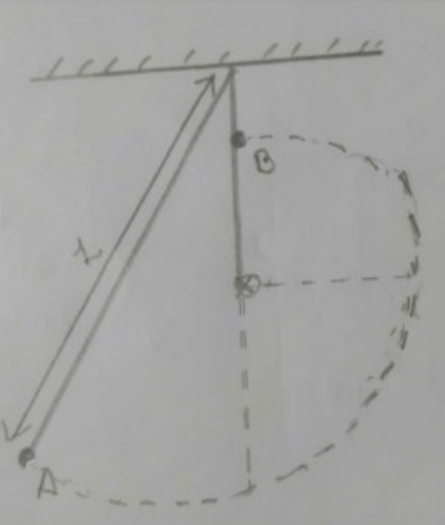
$\mathrm{K} \cdot \mathrm{E}_{\mathrm{A}}+\mathrm{P} \cdot \mathrm{E}_{\mathrm{A}}=\mathrm{K} \cdot \mathrm{E}_{\mathrm{B}}+\mathrm{P} \cdot \mathrm{E}_{\mathrm{B}}$
we get,
$P \cdot E_{A}=P \cdot E_{B}$
Thus maximum height is same as initial height.
(b)
At C, $1 / 2 \mathrm{mv}_{\mathrm{c}}{ }^{2}-0=\mathrm{mg}(\mathrm{L} / 2)(1-\cos \propto)$
$V_{c}=(\sqrt{g L}(1-\cos \alpha)) \ldots . .1$
Again,
$V_{c}=(\sqrt{g L} \cos \propto) \ldots . .2$
equating 1 and 2
$\cos \alpha=2 / 3 \ldots . .3$
Now, BF $=\frac{\stackrel{L}{2}}{\frac{L}{2}}+{ }^{\frac{L}{2}} \cos \propto$
$\mathrm{BF}=(5 \mathrm{~L} / 6)$
(C)
$\left(\mathrm{mv}_{\mathrm{c}}^{2}\right) / \mathrm{L}-\mathrm{x}=\mathrm{mg}$
$\mathrm{V}_{\mathrm{c}}=(\sqrt{\mathrm{g}}(\mathrm{L}-\mathrm{x})) \ldots 1$
Also,
$1 / 2 \mathrm{mv}_{\mathrm{c}}{ }^{2}-0=\mathrm{mg}(\mathrm{OC})$
$\mathrm{V}_{\mathrm{c}}=(\sqrt{2} \mathrm{~g}(2 \mathrm{x}-\mathrm{L})) \ldots . .2$
Equating 1 and 2
$g(L-x)=2 g(2 x-L)$
$x / L=0.6$
