A cart of mass $M$ is at rest on a frictionless horizontal surface and a pendulum bob of mass $m$ hangs from the roof of the cart. The string breaks, the bob falls on the floor, makes several collisions on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is $\mathrm{L}$. Find the displacement of the cart during this process.
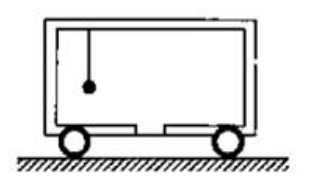
Take ${ }^{\circ}$ as origin
$x_{C O M}=\frac{x m+(x+L) M}{m+M}$
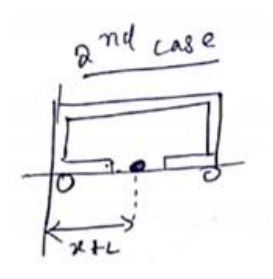
$x_{C O M}^{\prime \prime}=(x+L) \frac{(m+M)}{(m+M)}$
$\left|x_{\operatorname{COM}}^{\prime}-x_{\text {COM }}\right|=x+L-\left[\frac{x m+(x+L) M}{m+M}\right\rfloor$
$=\frac{x m+M x+L m-x m-x M-L M}{m+M}$
$=\frac{L m}{m+M}$
Cart should be displaced $\frac{}{\frac{L m}{m+M}} \mathrm{Cm}$ for COM of system to be same.
