Question:
A solid sphere of mass $0.50 \mathrm{~kg}$ is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is $2 / 7$. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
Solution:
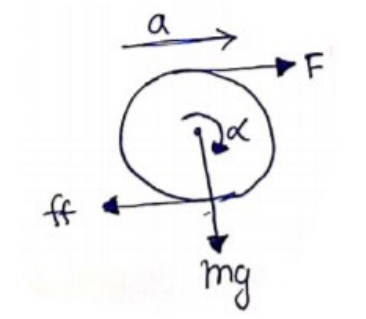
$F-f f=m a$
$\tau=I \alpha$
$(F R+f f R)=\left(\frac{2}{5} m R^{2}\right)\left(\frac{a}{R}\right)$
$F+f f=\frac{2}{5} m a$
$f f=\mu \mathrm{ii})$
Solving (i),(ii) and (iii)
$\mathrm{F}=3.3 \mathrm{~N}$
