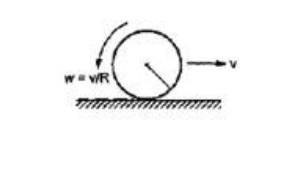
A solid sphere is set into motion on a rough horizontal surface with a linear speed $v$ in the forward direction and an angular speed $v / R$ in the anticlockwise direction as shown in figure. Find the linear speed of the sphere (a) when it stops rotating and (b) when slipping finally ceases and pure rolling starts.
Conserving angular momentum about bottom point $L_{i}=L_{f}$
$m v R-I \omega=m v^{\prime} R$
$m v R-\left(\frac{2}{5} m R^{2}\right)\left(\frac{v}{R}\right)=m v^{\prime} R$
$\frac{3}{5} m v R=m v^{\prime} R$
$v^{\prime}=\frac{3 v}{5}$
Conserving angular momentum
$m v^{\prime} R=m v^{\prime \prime} R+I \omega^{n}$
$m\left(\frac{3 v}{5}\right) R=m v^{n} R+\left(\frac{2}{5} m R^{2}\right)\left(\frac{v !}{R}\right)$
$v^{m}=\frac{3 w}{7}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.