Question:
A block of mass $\mathrm{m}$. is attached to two upstretched springs of spring constants $\mathrm{k}$, and $\mathrm{k} 2$ as shown in figure (8-E9). The block is displaced towards right through a distance $x$ and is released. Find the speed of the block as it passes through the mean position shown.
Solution:
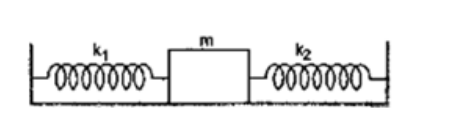
By law of conservation of energy
$\frac{1}{2} \mathrm{~m} \mathrm{v}^{2}=\frac{\overline{1}}{2} \mathrm{k}_{1} \mathrm{x}^{2}+\frac{\overline{1}}{2} \mathrm{k}_{2} \mathrm{x}^{2}$
So, $\left.v=x \sqrt{\left(\mathrm{k}_{1}\right.}+\mathrm{k}_{2}\right) / \mathrm{m}$
