Question:
The pulleys in figure are identical each having a radius $\mathrm{R}$ and moment of inertia $\mathrm{I}$. Find the acceleration of block $M$.
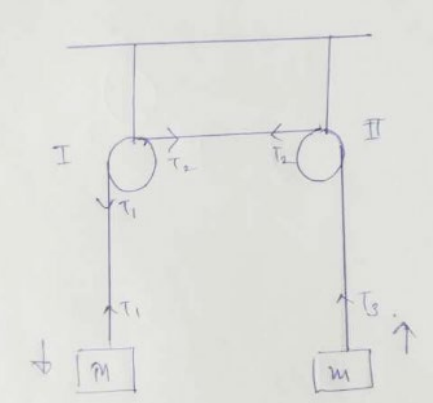
Solution:
$m g-T_{1}=m a-\cdots--(i)$
$\left(T_{1}-T_{2}\right) r_{1}=I \alpha$
$a=\alpha r$
$\left(T_{1}-T_{2}\right)=\frac{I \alpha}{R^{2}}$ For pulley $1-\cdots-($ ii $)$
$\left(T_{2}-T_{3}\right)=\frac{I \alpha}{R^{2}}$ For pulley $2 \cdots-\cdots($ iii $)$
For block of mass $m$
$T_{3}-m g=m a----(i v)$
$\mathrm{T}_{1}-T_{3}=\frac{2 I \alpha}{R^{2}}-\cdots-(i v)$
Adding equation (i) ans (iv)
$-m g+M g+\left(T_{3}-T_{1}\right)=M a+m a$
$M g-m g=M a+m a+\frac{I \alpha}{R^{2}}$
$\mathrm{Mg}-\mathrm{mg}=\mathrm{Ma}+\mathrm{ma}+\frac{1 \alpha}{R^{2}}$
$a=\frac{(M-m) g}{M a+m a+\frac{I \alpha}{R^{2}}}$
