Question:
A metric stick is held vertically with one end on a rough horizontal floor. It is gently allowed to fall on the floor. Assuming that the end at the floor does not slip, find the angular speed of the rod when it hits the floor.
Solution:
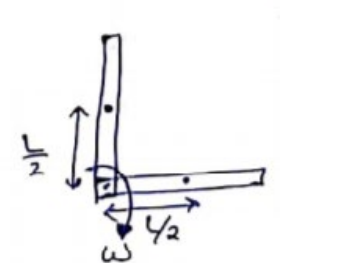
By energy conservation
$\mathrm{mg}^{2}=\frac{1}{2} I \omega^{2}$
$m a^{2} \frac{L}{2}=\frac{1}{m L^{2}}\left(\frac{\omega^{2}}{3}\right) \omega^{2}$
$\omega=\sqrt{\frac{3 g}{l}}=\sqrt{3 \times \frac{9.8}{1}}$
$\omega=5.42 \mathrm{rad} / \mathrm{sec}$
