Two blocks of masses $10 \mathrm{Kg}$ and $20 \mathrm{Kg}$ are placed on the X-axis. The first mass is moved on the axis by a distance of $2 \mathrm{~cm}$. By what distance should the second mass be moved to keep the position of the center of mass unchanged?
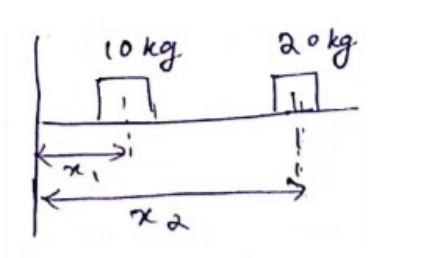
Initially, let
$10 \mathrm{Kg}$ be ${ }^{x_{1}} \mathrm{Cm}$ away
$20 \mathrm{Kg} \mathrm{be}{ }^{x_{2}} \mathrm{~cm}$ away
$\therefore x_{C O M}=\frac{10 x_{1}+20 x_{2}}{30}$
$\therefore x_{C O M}=\frac{10 x_{1}+20 x_{2}}{30}$
Let $20 \mathrm{Kg}$ be moved by distance of $2 \mathrm{~cm}$.
$\therefore x_{C O M}^{z}=\frac{\left(x_{1}+2\right) 10+20\left(x_{2}+\alpha\right)}{30}$
$x_{\mathrm{COM}}^{z}=x_{\mathrm{COM}}$
$\Rightarrow 10 x_{1}+20 x_{2}=10 x_{1}+20+20 x_{2}+20 \alpha$
$\Rightarrow \alpha=-1_{\mathrm{cm}}$
$20 \mathrm{Kg}$ should move $1 \mathrm{~cm}$ towards left.
