Question:
A sting is wrapped on a wheel of moment of inertia $I=0.20 \mathrm{kgm}{ }^{2}$ and radius $10 \mathrm{~cm}$ and goes through a light pulley to support a ablock of mass $2.0 \mathrm{~kg}$ as shown in the figure. Find the acceleration of the block
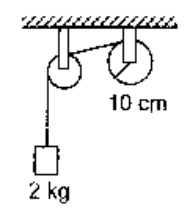
Solution:
Moment of inertia of the pulley. $I=0.20 \mathrm{kgm}^{2}$
From the diagram we get
$m g-T=m a-\cdots-(i)$
$\operatorname{Tr}=\mathrm{I} \alpha$
$a=\alpha r$
$\mathrm{T}=\frac{\mathrm{I} \alpha}{r^{2}}-----(i i)$
$U \sin g$ equation (i) ans (ii)
$m g=\left(m+\frac{I}{r^{2}}\right) \alpha$
$a=\frac{m g}{m+\frac{I}{r^{2}}}$
$a=\frac{2 \times 9.8}{2+\frac{0.2}{0.01}}$
$a=\frac{19.6}{22}=0.89 \mathrm{~ms}^{-2}$
