Question:
Figure shows two blocks of masses $m$ and $M$ connected by a string passing over a pulley. The horizontal table over which the mass $m$ slides is smooth. The pulley has a radius $r$ and moment if inertia I about its axis and it can freely rotate about the axis. Find the acceleration of the mass $M$ assuming that the string does not slip on the pulley.
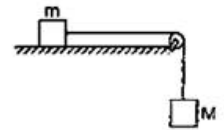
Solution:
$\mathrm{Mg}_{-} T_{2}=\mathrm{Ma}-(\mathrm{i})$
$\mathrm{T}_{2} r-T_{1} r=I \alpha$
$T_{1}=m a$-(iii)
$a=r a-(i v)$
Solving, (i),(ii),(iii) and (iv)
$\quad \frac{M g}{M+m+\frac{I}{r^{2}}}$
$a={ }^{a=}$
