A car moving at a speed of $36 \mathrm{~km} / \mathrm{hr}$ is taking a turn on a circular road of radius $50 \mathrm{~m}$. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road (figure 7-E4). A small block of mass $100 \mathrm{~g}$ is kept on the seat which rests against the plate. The friction coefficient between the block and the plate is $1.1=0.58$. (a) Find the normal contact force exerted by the plate on the block. (b) The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
(a)
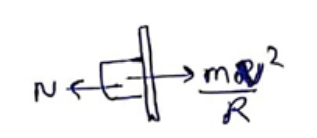
$N=\frac{m v^{2}}{R}$
$=\frac{(0.1)\left(36 \times \frac{5}{18}\right)^{2}}{50}$
$\mathrm{N}=0.2$
(b)
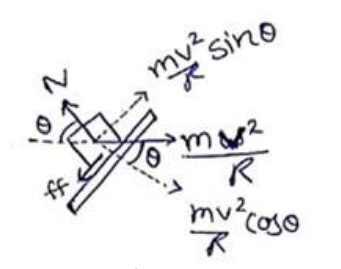
At the time of just sliding
$\mathrm{ff}=\frac{m v^{2}}{R} \sin \theta$
$\mu \mathrm{N}=\frac{m v^{2}}{R} \sin \theta$
$\frac{\mu m v^{2}}{R} \cos \theta=\frac{m v^{2}}{R} \sin \theta$
$\mu=\tan \theta$
$\theta=\tan -1(0.58)$
$\theta=300$
