Question:
A uniform disc of radius $\mathrm{R}$ is put over another uniform disc of radius $2 \mathrm{R}$ of the same thickness and density. The peripheries of the two discs touch each other. Locate the center of mass of the system.
Solution:
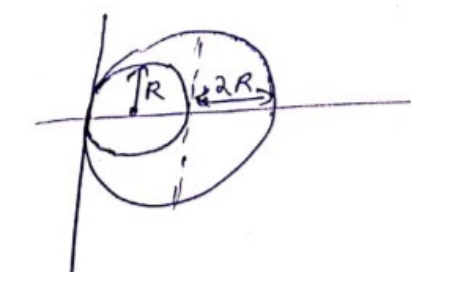
C.O.M of $2 \mathrm{R}$ disc $=(2 \mathrm{R}, 0)$
C.O.M of $R$ disc $=(R, 0)$
$=\frac{m_{2 R^{x}}{ }^{x}+m_{R^{x} R}}{m_{n R}+m_{R}}$
$\left\{m_{2 R}=\rho .4 \pi(2 R)^{2}\right\}$
$\left\{m_{R}=\rho .4 \pi R^{2} l\right\}$
$=\frac{\left(\rho 4 \pi l R^{2}\right) \cdot(2 R)+\left(\rho 4 \pi l R^{2}\right) \cdot(R)}{\rho 4 \pi R^{2} l(4+1)}$
$=\frac{8 R+R}{5}=\frac{9 R}{5}$
Distance of C.O.M (system) from C.O.M of $2 R$ disc
$=2 R-\frac{9 R}{5}=\frac{R}{5}$
