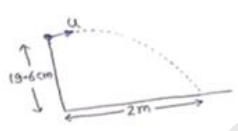
A popular game in Indian villages is goli which is played with small glass balls called golis. The goli of one player is situated at a distance of $2.0 \mathrm{~m}$ from the goli of the second player. The second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is $19.6 \mathrm{~cm}$ from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationary goli without falling on the ground earlier?
$x$-axis $y$-axis
$s_{x}=2 m u_{y}=0$
$a_{x}=0 a_{y}=g$
$s_{y}=19.6 \mathrm{~cm}$
$S_{y}=u_{y} t+\frac{1}{2} a_{y} t^{2}$
$\frac{19.0}{100}=0+\frac{1}{2}(9.8) t^{2}$
$s_{x}=u_{x} t+\frac{1}{2} a_{x} t^{2} t=0.2 s e c$
$2=u_{x} t+\frac{1}{2} a_{x} t^{2}$
$2=u_{x}(0.2)+0$
$u_{x}=10 \mathrm{~m} / \mathrm{s}$
