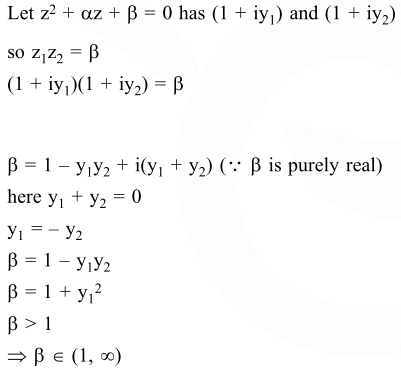Question: Let $\alpha, \beta$ be real and $z$ be a complex number. If $z^{2}+\alpha z+\beta=0$ has two distinct roots on the line $\operatorname{Re} z=1$, then it is necessary that :-
$|\beta|=1$
$\beta \in(1, \infty)$
$\beta \in(0,1)$
$\beta \in(-1,0)$
Correct Option: , 2
Solution: